写像。その定義。集合Xと集合Yが与えられているとする。Xの各要素xに対し、ある規則によって対応する、Yの要素yがただ1つ存在するとき、この対応をXからYへの写像であるという。

集合Xの要素xの中に1つでも対応するYの要素がない場合には写像ではない。

全ての要素xに対して対応するYの要素がただ1つ存在しなければならない。逆にあるxに対応するYの要素が2つある場合も写像ではない。

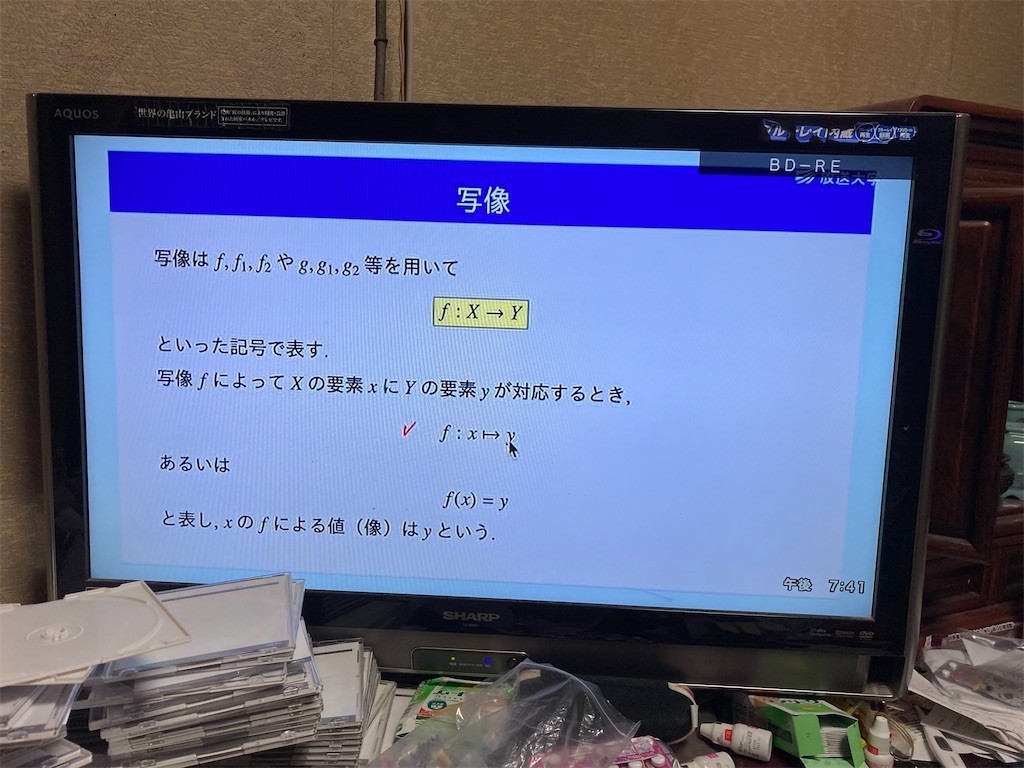
写像はf,f1,f2やg,g1,g2(fやgや添字)等を用いてf:X→Yといった記号で表す。XからYへの写像。写像fによって集合Xの要素xに対して集合Yの要素yが対応するとき、f:x→yあるいはf(x)=yと表し、xのfによる値(像)はyという。
写像fをxからyへの写像、f:x→yとする。Xの全体をfの定義域と呼ぶ。そして集合Xのfによる像、f(X)={y|y=f(x)かつx∈X}をfの値域という。集合Xの中の各要素xの像を全て集めた集合をfの値域と。一般に値域f(x)はYの部分集合となる。Yの中には値域でないものもある場合がある。対応していないものは値域ではない。次にf:X→Yとする。Xの部分集合X'のfによる像f(X')の定義。f(X')={y|y=f(x)かつx∈X'}。元になる要素がX'にないと外れる。また同様に、Yの部分集合Y'のfによる逆像の定義。f^-1(Y')={x|f(x)∈Y'}。f(x)がY'の要素となるようなxを全て集めた集合f^-1。fとgの合成写像。集合X,Y,Zに対し、2つの写像f:X→Yとg:Y→Zが与えられているとする。この写像g○f:X→Zをg○f(x)=g(f(x))で定義する。xはXの要素である。このfの像を求めた次にgの像を求めた写像g○fをfとgの合成写像という。書く時にはfとgの順序が逆になることに注意。f(x)に対してgを適用する。f(x)に対するgの像。g○fを単にgfとも書く。写像f:X→Yとする。任意のx,x'∈Xに対して、x≠x'(別のもの)ならばf(x)≠f(x')であるとき、写像fは単射(1対1)であるという。xが異なるならその像f(x)も異なdるということ(同じ要素にはならない)。x1≠x2(2つの要素が異なる場合)ならf(x1)≠f(x2)である。