ここでも根底となりそうな概念が。内積は高校でも親しんだけど直積はあまり聞かない。
順序対。xとyを、順序を考慮して並べた組を順序対といい、(x,y)で表す。2つの順序対が等しい、(x,y)=(u,v)⇔x=uかつy=v。一般に、順序対(x,y)と(y,x)は等しくない、(x,y)≠(y,x)。2つの要素がある集合同士は等しい、{x,y}={y,x}。例。順序対(3,5)と順序対(5,3)は異なるもの。集合{3,5}と集合{5,3}は要素が同じなので同じもの。
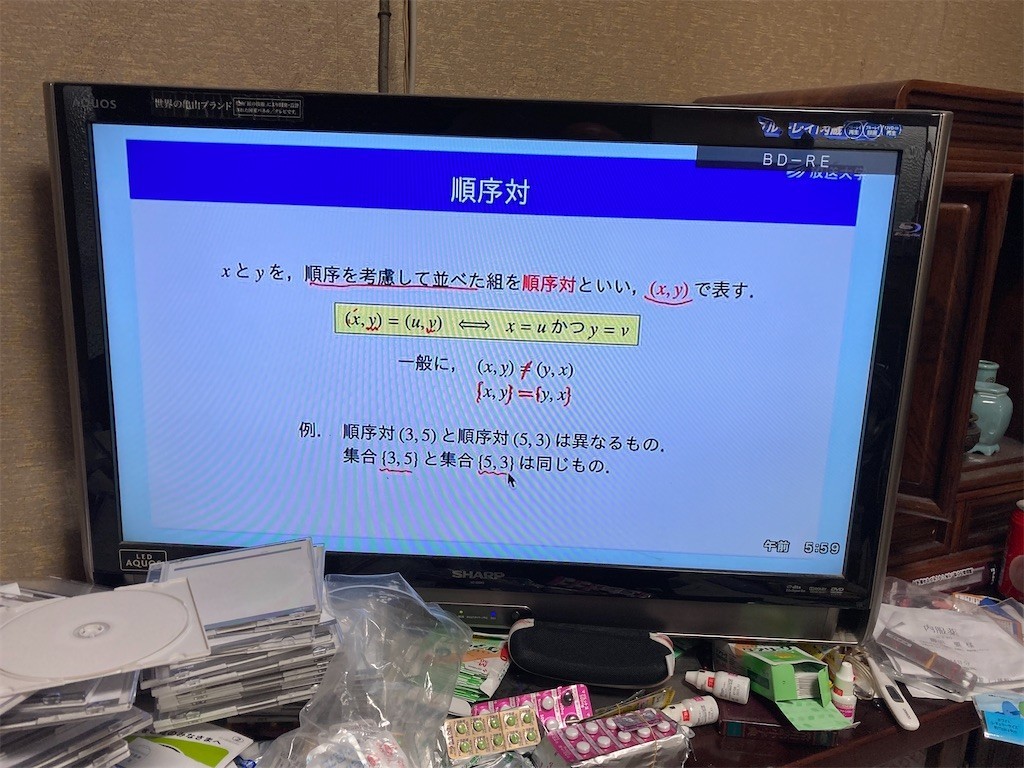
順序列。同様に拡張して、3つの対象x,y,zを順序を考慮して一列に並べた組を順序列といい、(x,y,z)で表す。
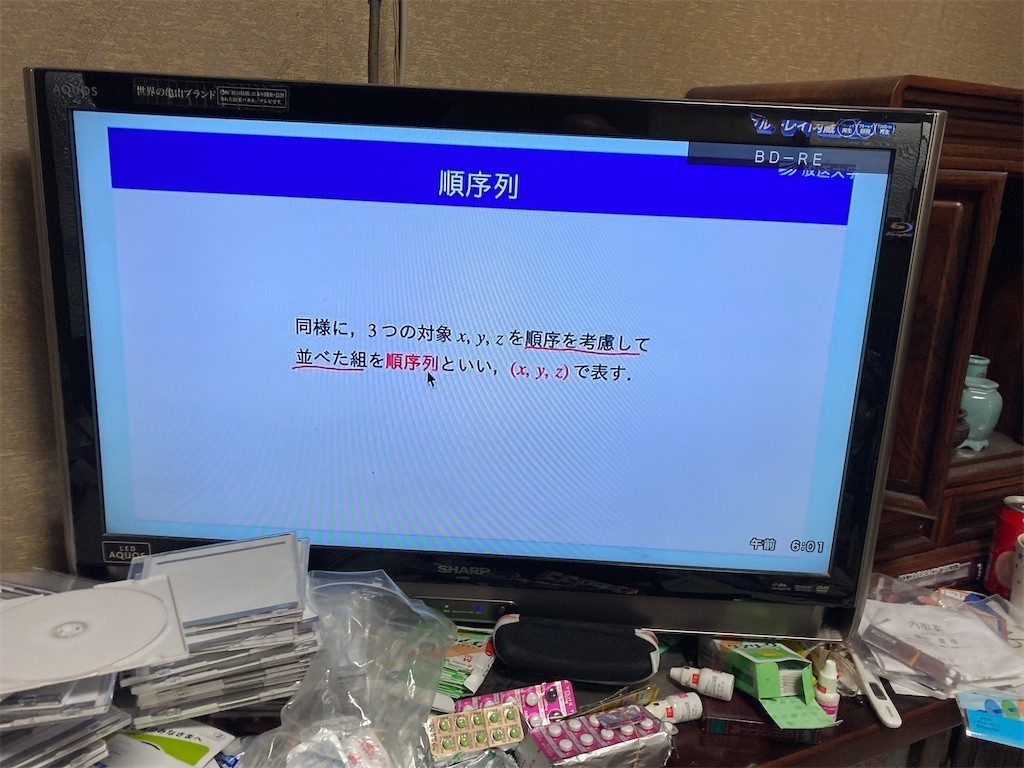
今の話を拡張して一般化する。n個の対象x1,x2,…,xnを、順序を考慮して一列に並べた組を順序列といい、(x1,x2,…,xn)で表す。2つの順序列が等しいということ、(x1,x2,…,xn)=(y1,y2,…,yn)⇔x1=y1,x2=y2,…,xn=yn。全ての式が成立するときに2つの順序列が等しい。
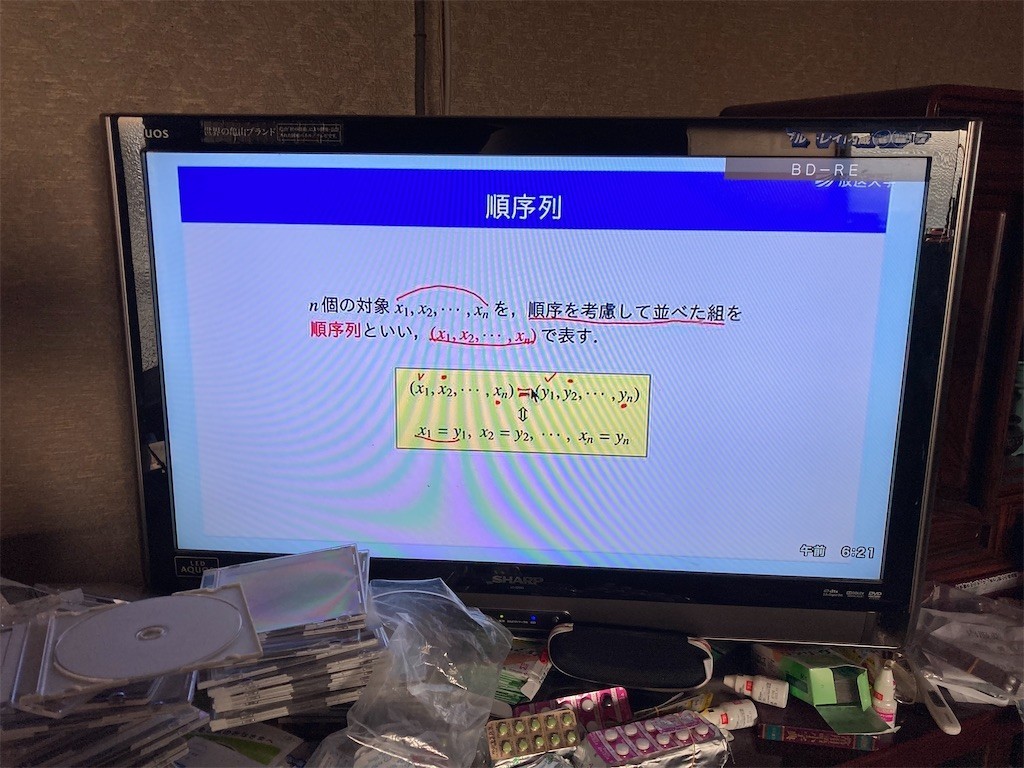
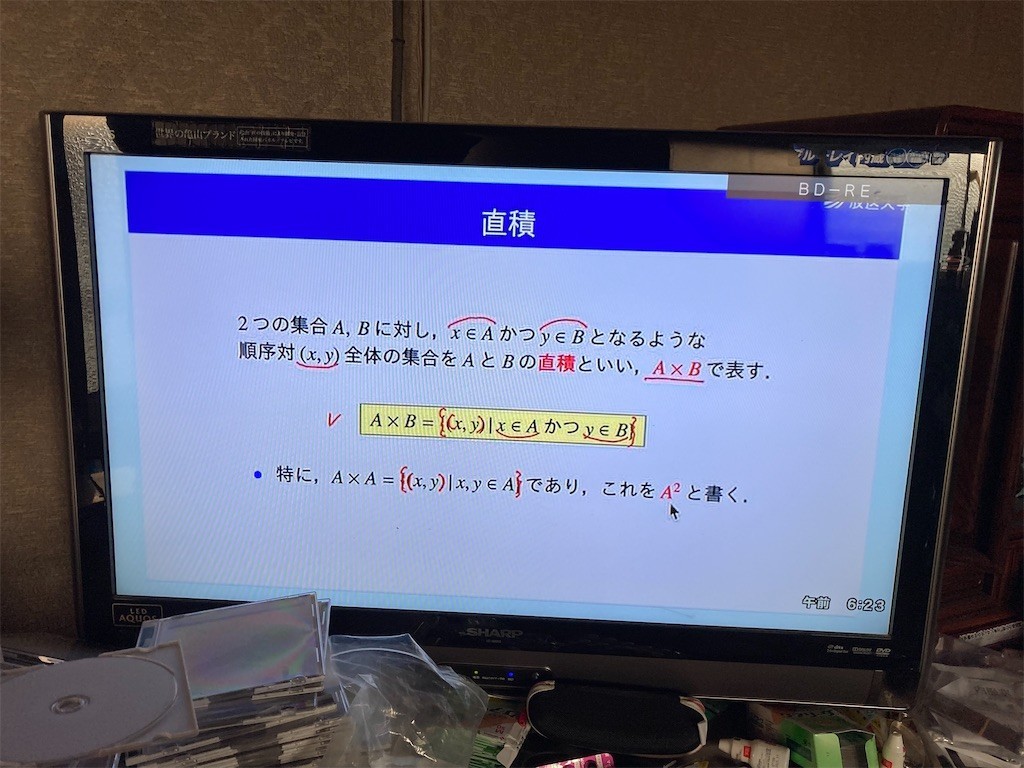
直積。2つの集合A,Bに対し、x∈Aかつy∈Bとなるような順序対(x,y)全体の集合をAとBの直積といい、A×Bで表す。A×B={(x,y)|x∈Aかつy∈B}。特にA×A={(x,y)|x,y∈A}であり、これをA^2と書く(Aの2乗積、Aの2乗と呼ぶ)。
これを一般化。n乗積。各々のi(1≦i≦n)においてxi∈Aとなるような順序列(x1,x2,…,xn)全体の集合をAのn乗積といい、A^nで表す。

直積の例を挙げる。A:あるレストランのケーキの種類全体の集合、B:飲み物の種類全体の集合、A×B:ケーキと飲み物の組み合わせ(順序対)全体の集合。

集合は図示したり具体例を具体的に考えると分かりやすい。
直積は数の掛け算としての積とは違うけど、表し方がA×BやA^2など数としての表し方と同じなので混同しないように注意。Aをケーキの種類全体の集合とすると、A×A(つまりAの2乗)はケーキとケーキの組み合わせ方全体の集合。
最初のケーキを篠崎菜穂子さん、2つ目のケーキを隈部正博さんが食べる場合には2つのケーキの順序対という概念が必要となる。しかし単にケーキを2つ買った場合は順序対を考える必要はない。この2つの例の違いに注意。
順序対と順序列。順序対は2つのものの順序を考える。3つ以上は順序列。いずれの場合も順序を考慮して一列に並べる考え方であることが重要。
